3.1. Основные понятия теории игр

Определив предмет институционализма как анализ взаимодействия индивидов и структур, его обеспечивающих, необходимо обратиться к вопросу о методе. Математический аппарат, традиционно используемый экономистами (дифференциальное исчисление), вряд ли приемлем в качестве базового метода в анализе взаимодействий. Главным образом потому, что использование этого аппарата обосновывается рядом утверждений из «жесткого ядра» неоклассики, с которыми соглашаются далеко не все институционалисты: полной рациональностью индивидов; существованием, единственностью и Парето-оптимальностью равновесия; экзогенным характером предпочтений, описываемых ординалистской теорией предельной полезности.

Формальные модели в институциональной экономике строятся с помощью теории игр, развитие которой берет отсчет с момента появления книги Дж. фон Неймана и О. Моргенштерна «Теория игр и экономическое поведение» (1944). Во-первых, теория игр занимается анализом ситуаций, в которых поведение индивидов взаимообусловлено: решение каждого из них оказывает влияние на результат взаимодействия и. следовательно, на решения остальных индивидов. Решая вопрос о своих действиях, индивид вынужден ставить себя на место контрагентов. Во-вторых, теория игр не требует полной рациональности индивидов, в ней используется целый ряд моделей индивидов, от индивида как совершенного калькулятора до индивида как робота. В-третьих, теория игр не предполагает существования, единственности и Парето-оптимальности равновесия во взаимодействиях. Эти причины и обусловливают наш интерес к формальным моделям институтов, построенным с помощью теории игр. Обратимся к их анализу более подробно.

Первое уточнение касается кооперативных и некооперативных игр. В кооперативных играх возможны обмен информации между участниками и формирование коалиций. В некооперативных играх, о которых и пойдет в основном речь, исходным пунктом в анализе является индивидуальный участник, причем обмен информации между участниками и формирование коалиций исключены. Далее, игра может быть представлена либо в стратегической (матричной), либо в развернутой форме. Например, вернемся к упомянутой в предыдущих лекциях «дилемме заключенных» (рис. 5.1).

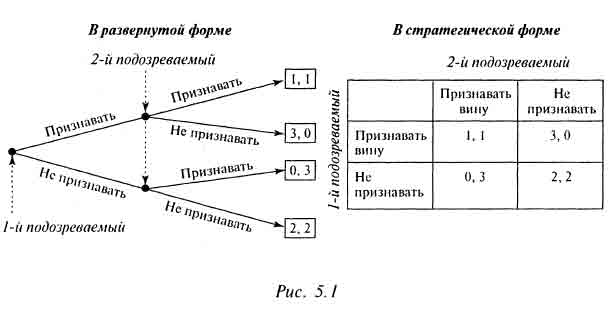
Первые цифры в описании результатов взаимодействия отражают полезность первого участника, вторые — второго: U₁ (признавать, при условии, что второй не признает) = 3. Напомним, что здесь речь идет о «полезности» различных сроков осуждения, которая обратно пропорциональна их величине.

Типы равновесий

В каждом взаимодействии могут существовать различные виды равновесий: равновесие доминирующих стратегий, равновесие по Нэшу, равновесие по Штакельбергу и равновесие по Парето. Доминирующей стратегией называется такой план действий, который обеспечивает участнику максимальную полезность вне зависимости от действий другого участника Соответственно, равновесием доминирующих стратегий будет пересечение доминирующих стратегий обоих участников игры. Равновесие по Нэшу — ситуация, в которой стратегия каждого из игроков является лучшим ответом на действия другого игрока. Иными словами, это равновесие обеспечивает игрока максимумом полезности в зависимости от действий другого игрока. Равновесие по Штакельбергу возникает тогда, когда существует временной лаг в принятии решений участниками игры: один из них принимает решения, уже зная, как поступил другой. Таким образом, равновесие по Штакельбергу соответствует максимуму полезности игроков в условиях неодновременности принятия ими решений. В отличие от равновесия доминирующих стратегий и равновесия по Нэшу этот вид равновесия существует всегда. Наконец, равновесие по Парето существует при условии, что нельзя увеличить полезность обоих игроков одновременно. Рассмотрим на одном из примеров технологию поиска равновесий всех четырех видов.

Доминирующая стратегия — такой план действий, который обеспечивает участнику максимальную полезность вне зависимости от действий другого участника.

Равновесие по Нэшу — ситуация, в которой ни один из игроков не может увеличить свой выигрыш в одностороннем порядке, меняя свой план действий.

Равновесие по Штакельбергу — ситуация, когда ни один из игроков не может увеличить свой выигрыш в одностороннем порядке, а решения принимаются сначала одним игроком и становятся известными второму игроку.

Равновесие по Парето — ситуация, когда нельзя улучшить положение ни одного, из игроков, не ухудшая при этом положения другого и не снижая суммарного выигрыша игроков.

Пусть фирма А стремится нарушить монополию фирмы Б на выпуск определенного продукта. Фирма А решает, стоит ли ей входить на рынок, а фирма Б — стоит ли ей снижать выпуск в том случае, если А все же решает входить. В случае неизменного выпуска на фирме Б обе фирмы в проигрыше, если же фирма Б решает снизить выпуск, то она «делится» своей прибылью с А.

Равновесие доминирующих стратегий. Фирма А сравнивает свой выигрыш при обоих вариантах развития событий (-3 и 0, если Б решает развязать ценовую войну) и (4 и 0, если Б решает снизить выпуск). У нее нет стратегии, обеспечивающей максимальный выигрыш вне зависимости от действий Б: 0 > -3 ⇒ «не входить на рынок», если Б оставляет выпуск на прежнем уровне, 4 > 0 ⇒ «входить», если Б снижает выпуск (см. сплошные стрелки). Хотя у фирмы А нет доминирующей стратегии, у Б такая стратегия есть. Она заинтересована снижать выпуск вне зависимости от действий А (4 > -2, 10 ≡ 10, см. пунктирные стрелки). Следовательно, равновесие доминирующих стратегий отсутствует.

Равновесие по Нэшу. Лучший ответ фирмы А на решение фирмы Б оставить выпуск прежним — не входить, а на решение снизить выпуск — входить. Лучший ответ фирмы Б на решение фирмы А войти на рынок — снизить выпуск, при решении не входить — обе стратегии равнозначны. Поэтому два равновесия по Нэшу (N₁, N₂) находятся в точках (4, 4) и (0, 10) — А входит, а Б снижает выпуск, или А не входит, а Б не снижает выпуск. Убедиться в этом достаточно легко, так как в этих точках никто из участников не заинтересован в изменении своей стратегии.

Равновесие по Штакельбергу. Предположим, первой принимает решение фирма А. Если она выбирает входить на рынок, то в конечном счете окажется в точке (4, 4): выбор фирмы Б однозна­чен в этой ситуации, 4 > -2. Если она решает воздержаться от входа на рынок, то итогом будут две точки (0, 10): предпочтения фирмы Б допускают оба варианта. Зная это, фирма А максимизирует свой выигрыш в точках (4, 4) и (0, 10), сравнивая 4 и 0. Предпочтения однозначны, и первое равновесие по Штакельбергу St_A будет находиться в точке (4, 4). Аналогичным образом, равновесие по Штакельбергу St_Б, когда первой принимает решение фирма Б, будет находиться в точке (0, 10).

Равновесие по Парето. Чтобы определить оптимум по Парето, мы должны последовательно перебрать все четыре исхода игры, отвечая на вопрос: «Обеспечивает ли переход к любому другому исходу игры увеличение полезности одновременно для обоих участников?» Например, из исхода (-3, -2) мы можем перейти к любому другому исходу, выполняя указанное условие. Только из исхода (4, 4) мы не можем двинуться дальше, не уменьшая при этом полезности ни одного из игроков, это и будет равновесием по Парето, Р.

Классификация моделей

Теперь рассмотрим несколько базовых для теории игр моделей. Эти модели отличаются количеством точек равновесия по Нэшу и их совпадением или несовпадением с точками равновесия по Штакельбергу и по Парето. В общем виде типология моделей для двух участников, используемых в теории игр, будет выглядеть следующим образом:

Модель I касается выбора двумя студентами места встречи: каждого из них при желании можно найти либо в библиотеке, либо в буфете. Предполагается, что встреча в буфете обеспечит обоим студентам большую полезность, они смогут сопроводить ее чашкой кофе или кружкой пива:

Эта игра особенно интересна в связи с тем, что с ее помощью иллюстрируется идея «фокальной точки» — спонтанно выбираемого обоими студентами места встречи: Если оба хорошо знают друг друга, то им не составит особого труда предположить место, где они смогут найти друг друга. По всей вероятности «фокальной точкой» чаще всего будет буфет.

Модель II иллюстрируется ситуацией «конфликта между супругами в жесткой форме». Супруги решают, каким образом провести вечер, выбирая между двумя альтернативами — идти на концерт или на футбольный матч. Индивидуальные предпочтения очевидны: жена предпочитает концерт, муж — матч, и при этом супруги достаточно низко оценивают удовольствие от совместно проведенного вечера:

Игра интересна тем, что здесь у обоих участников есть доминирующая стратегия (х), идти на концерт — для супруги, идти на матч — для супруга.

Следующая модель III — уже обсуждавшаяся «дилемма заключенных»:

Модель IV является вариацией по поводу конфликта между супругами, но на этот раз в мягкой форме. Единственное отличие от конфликта в жесткой форме — супруги высоко оценивают удовольствие от совместно проведенного вечера:

«Проблема разоружения» иллюстрирует модель V. Страна А решает вопрос, развязывать ли войну в отношении страны Б или нет, страна же Б выбирает, вооружаться ли ей или разоружаться. Проблема в том, что разоруженная страна Б станет легкой добычей для агрессора А, а вооруженная сможет адекватно ответить на агрессию:

Ситуация тяжелого морального выбора, связанного с принятием решения о просмотре эротического фильма «9 1/2 недель», является иллюстрацией модели VI. Первый потенциальный зритель будет сожалеть, если ему не удастся увидеть фильм, но если он его все же начинает смотреть, то ему становится стыдно. Для второго зрителя, ханжи, просмотр фильма следует запретить всем, но если уж его смотреть, то только ему одному.

Модель VII может быть представлена в форме следующей игры. Каждый игрок в начале игры имеет 2 дол. и кладет половину этой суммы в коробку. Затем коробка передается первому игроку, который может либо оставить ее себе, либо выбросить в колодец. Второй участник должен предсказать поведение первого, и если ему это удается, то он получает 1 дол. (который оставался у первого). Если же ему не удается угадать, то он отдает первому игроку остававшийся у него доллар. Кроме того, если коробку не бросают в колодец, то игроки делят между собой находящуюся в ней сумму.

Наконец, взаимоотношения государства и инвестора описываются моделью VIII. У инвестора есть два варианта действий — инвестировать в стране или не инвестировать. Государство же может устанавливать высокое налогообложение доходов от инвестиций или отменить налоги вообще.

Выводы. Рассмотренные модели позволяют увидеть и проанализировать проблемы, возникающие в ходе взаимодействий индивидов:

• Проблема координации возникает в случае существования двух точек равновесия по Нэшу (модели I, IV). Решение проблемы координации связано с введением дополнительных институциональных условий, существования «фокальных точек» или соглашений. Например, согласование супругами своих действий существенно облегчается при наличии соглашения о приоритете интересов супруги.
• Проблема совместимости характерна для ситуаций, когда равновесие по Нэшу отсутствует (модели VII, VIII). Индивиды не могут согласовать свои действия, если институты не ограничивают и не «направляют» выбор стратегий. Например, введение во взаимоотношения государства и инвестора фактора репутации государства позволяет остановиться на исходе (2, 3).
• Проблема кооперации — равновесие по Нэшу существует, оно единственно, но Парето-неоптимально (модель III — «дилемма заключенных»). И в этой ситуации введение институционального ограничения, нормы «не признавать вину никогда», как мы уже видели на примере итальянской мафии, обеспечивает достижение оптимального по Парето результата.
• Проблема справедливости становится актуальной, если единственное равновесие по Нэшу характеризуется асимметричным, несправедливым распределением выигрыша между участниками взаимодействия (модели V, VI). Одним из вариантов решения проблемы несправедливости будет переход к повторяющимся играм и возникновение норм на основе «смешанных» стратегий, когда в момент времени t₀ индивид выбирает стратегию А, а в момент времени t₁ — стратегию Б и т.д.

3.2. Повторяющиеся игры

Смешанные стратегии

Обратимся к более подробному анализу повторяющихся игр. Когда игроки попадают в определенную ситуацию выбора неоднократно, то их взаимодействие существенным образом усложняется. Они могут позволить себе комбинировать стратегии, максимизируя общий выигрыш. Покажем это с помощью модели, описывающей отношения между Центральным банком (ЦБ) и экономическим агентом в связи с проводимой ЦБ кредитно-денежной политикой. К слову, эта ситуация интересна еще и в качестве примера использования теории игр для анализа конкретных экономических проблем. Итак, ЦБ ориентируется либо на жесткую кредитно-денежную политику, стремясь поддержать инфляцию на фиксированном уровне (π₀), либо на эмиссию и, следовательно, повышение темпов инфляции (π₁). В свою очередь, экономический агент действует на основе своих инфляционных ожиданий π_e (устанавливает цены на свою продукцию, решает вопросы о приобретении товаров и услуг и т.д.), которые могут либо подтверждаться, либо не подтверждаться в результате проводимой ЦБ политики. В случае если π₁ > π_e, ЦБ получает прибыль от сеньоража и от инфляционного налога. π_e = π₁, то в проигрыше оказывается и ЦБ из-за сокращения поступлений от сеньоража, и экономические агенты, которые продолжают нести тяжесть инфляционного налога. Если π_e = π₀, то сохраняется статус-кво и в проигрыше никто не оказывается. Наконец, если π_e > π₀, то проигрывают только экономические агенты: производители — из-за потери спроса на необоснованно подорожавшую продукцию, потребители — из-за создания неоправданных запасов.

Предложенная модель практически идентична по своей структуре базовой модели VIII: при однократном взаимодействии у агентов нет доминирующих стратегий, отсутствует и равновесие по Нэшу. При повторяющемся многократно взаимодействии, а именно такое взаимодействие и характерно для реальных ситуаций, оба участника могут использовать и ту, и другую имеющуюся у них в распоряжении стратегии. Позволяет ли игрокам чередование стратегий в определенной последовательности максимизировать свою полезность, т.е. достичь равновесия по Нэшу в смешанных стратегиях: исхода, при котором ни один участник не может увеличить свой выигрыш, изменяя в одностороннем порядке свою стратегию? Предположим, что ЦБ проводит жесткую кредитно-денежную политику с вероятностью Р₁ (в Р₁ % случаев), а с вероятностью (1 — Р₁) — инфляционную политику. Тогда при выборе экономическим агентом неинфляционных ожиданий (π_e = π₀) ЦБ может рассчитывать на получение выигрыша, равного EU(ЦБ) = Р₁0 + 1 (1 — Р₁) = 1 — Р₁. В случае инфляционных ожиданий у экономического агента выигрыш ЦБ составит EU(ЦБ) = Р₁0 + (1 — Р₁)(—2) = 2Р₁ - 2. Теперь допустим, что экономический агент имеет неифляционные ожидания с вероятностью Р₂ (в Р₁ % случаев), а инфляционные ожидания — с вероятностью (1 — Р₁). Отсюда ожидаемая полезность ЦБ в итоге составит EU(ЦБ) = Р₂(1 - Р₁) + (1 - Р₂)(2Р₁ - 2) = 3Р₂ - 3Р₁ Р₂ + 2Р₁ - 2. Аналогичные расчеты для экономического агента дадут EU(э.а.) = Р₁(Р₂ - 1) + (1 - Р₁)(-Р₂ - 2) = 2Р₁ Р₂ + Р₁ - Р₂ - 2. Если мы перепишем данные выражения в следующей форме EU(ЦБ) = Р₁(2 - 3Р₂) + 3Р₂ - 2 и EU(э.а.) = Р₂ (2Р₁ - 1) + Р₁ - 2, то нетрудно заметить, что при Р₂ — 2/3 выигрыш ЦБ не зависит от его собственной политики, а при Р₁ = 1/2 выигрыш экономического агента не зависит от его ожиданий.

Иными словами, равновесием по Нэшу в смешанных стратегиях будет формирование экономическим агентом в 2/3 случаев неинфляционных ожиданий и проведение ЦБ в половине случаев жесткой кредитно-денежной политики. Найденное равновесие достижимо при условии, что экономические агенты формируют ожидания рациональным образом, а не на основе инфляционных ожиданий в предыдущий период, скорректированных на ошибку прогноза предыдущего периода. Следовательно, изменения в политике ЦБ влияют на поведение экономических агентов только в той степени, в которой они неожиданны и непредсказуемы. Стратегия ЦБ в 50% случаев проводить жесткую кредитно-денежную политику, а в 50% — мягкую как нельзя лучше соответствует созданию атмосферы непредсказуемости. Интересно, что и России 90-х годов господствовал адаптивный тип инфляционных ожиданий, не обеспечивающий минимизацию проигрыша для экономических агентов при данных заложенных в модель условиях.

Эволюционно-стабильная стратегия

Разновидностью повторяющихся игр являются ситуации, когда индивид многократно попадает в определенную ситуацию выбора, но его контрагент не постоянен, а в каждом периоде индивид взаимодействует с новым визави. Поэтому вероятность выбора контрагентом той или иной стратегии будет зависеть не столько от конфигурации смешанной стратегии, сколько от предпочтений каждого из контрагентов. В частности, предполагается, что из общего числа N потенциальных контрагентов n (n/N%) всегда выбирают стратегию А, а m (m/N%) — стратегию Б. Тем самым создаются предпосылки для достижения нового типа равновесия, эволюционно-стабильных стратегий. Эволюционно-стабильной (ESS — Evolutionarily Stable Strategy) становится та стратегия, при которой если все члены определенной популяции используют ее, то никакая альтернативная стратегия не может ее вытеснить посредством механизма естественного отбора. Рассмотрим в качестве примера простейший вариант проблемы координации: разъезд на узкой дороге двух автомобилей (ситуация близка по некоторым параметрам и к модели I, и к модели IV). Предполагается, что в данной местности лево- и правосторонний стандарты движения равноправны (или же Правила дорожного движения просто не всегда выполняются). Автомобилю А движутся навстречу несколько автомобилей, с которыми ему нужно разъехаться. Если оба автомобиля принимают влево, въезжая на левую обочину по ходу движения, то они разъезжаются без проблем. То же самое происходит, если оба автомобиля принимают вправо. Когда же один автомобиль принимает вправо, а второй — влево и наоборот, то разъехаться они не смогут:

Итак, автомобилисту А известен приблизительный процент автомобилистов Б, систематически принимающих влево (Р), и процент автомобилистов Б, принимающих вправо (1 - Р). Условие для того, чтобы стратегия «принять вправо» стала для автомобилиста А эволюционно-стабильной, формулируется следующим образом: EU (вправо) > EU (влево), или 0Р + 1(1 - Р) > 1Р + 0(1 - Р), откуда Р < 1/2. Таким образом, при превышении доли автомобилистов во встречном потоке, принимающих вправо, уровня 50% эволюционно-стабильной стратегией становится «принять вправо» — сворачивать на правую обочину при каждом разъезде.

Эволюционно-стабильная стратегия — такая стратегия, что если ее использует^большинство индивидов, то никакая альтернативная стратегия не может ее вытеснить посредством механизма естественного отбора, даже если последняя более эффективна по Парето.

В общем виде требования к эволюционно-стабильной стратегии записываются следующим образом. Стратегия I, используемая контрагентами с вероятностью p, является эволюционно-стабильной для игрока тогда и только тогда, когда выполняются следующие условия: EU(I, р) > EU(J, p), что тождественно pU(I, I) + (1 - p)U(I, J) > pU(J, I) + (1 - p)U(J,J). Из чего следует:

• U(I, I) > U(J, I) или
• U(I, I) = U(J, I) и U(I, J) > U(J, J),

где — U(I, I) выигрыш игрока при выборе стратегии I, если контрагент выбирает стратегию I; U(J, I) — выигрыш игрока при выборе стратегии J, если контрагент выбирает стратегию I, и т.д.

Можно представить эти условия и в графической форме. Отложим по вертикальной оси ожидаемую полезность выбора той или иной стратегии, а по горизонтальной — долю индивидов в общей популяции игроков, выбирающих обе стратегии. Тогда мы получим следующий график (значения взяты из модели разъезда двух автомобилей), изображенный на рис. 6.1.

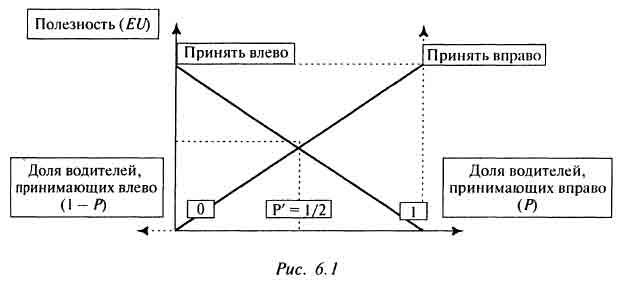
Из рисунка следует, что и «принять влево», и «принять вправо» имеют равные шансы на то, чтобы стать эволюционно-стабильной стратегией до тех пор, пока ни одна из них не охватила больше половины «популяции» водителей. Если же стратегия перешагивает этот рубеж, то она постепенно, но неизбежно вытеснит другую стратегию и охватит всю популяцию водителей. Дело в том, что, если стратегия перешагивает рубеж 50%, для любого водителя становится выгодным использовать ее в маневрах, что, в свою очередь, еще больше увеличивает привлекательность данной стратегии для остальных водителей. В строгой форме данное утверждение будет выглядеть следующим образом: dp/dt = G (EU (/, р) — EU (J, р)).

Главным результатом анализа повторяющихся игр является увеличение числа точек равновесия и решение на этой основе проблем координации, кооперации, совместимости и справедливости. Даже в дилемме заключенных, как мы уже упоминали в предыдущей лекции, переход к повторяющемуся взаимодействию позволяет достичь оптимального по Парето результата («отрицать вину»), не выходя за рамки нормы рациональности и запрета на обмен информацией между игроками. Именно в этом смысл «всеобщей теоремы» (folk theorem): любой исход, устраивающий индивида индивидуально, может стать при переходе к структуре повторяющейся игры равновесным. В ситуации дилеммы заключенных равновесным исходом при определенных условиях может стать и простая стратегия «не признавать», и множество смешанных стратегий. В числе смешанных и эволюционных стратегий, помимо Tit for Tat («зуб за зуб»), отметим следующие: Tlt-For-Two-Tats — начинать с отрицания вины и признавать вину, только если в два предшествующих периода кряду контрагент признавал вину; DOWING — стратегия, исходящая из предположения о равновероятном использовании контрагентом стратегий «отрицать вину» и «признавать» в самом начале игры. Далее каждое отрицание вины со стороны контрагента поощряется, а каждое признание — наказывается выбором стратегии «признавать вину» в следующий период; TESTER — начинать с признания вины, и если контрагент тоже признает вину, то в следующем периоде отрицать вину (т.е. извиниться) и далее использовать стратегию «зуб за зуб» — Tit for Tat.

Выводы. Подведем общие итоги обзора теории игр и вариантов ее использования в институциональном анализе. Главный аргумент в пользу того, чтобы строить модели институтов с помощью теории игр, заключается в интересе теории игр к ситуациям взаимозависимости действий индивидов, проблемам координации и согласования действий. Ведь именно институты призваны решить эти проблемы. С позиции теории игр функцию института можно определить как создание предпосылок (структурных, когнитив­ных, организационных) для фиксации одного из исходов игры в качестве равновесного. Эта задача особенно актуальна, если равновесие по Нэшу отсутствует или оно не единственно. Достижение равновесия с помощью институтов подразумевает:

• увеличение числа точек равновесия через формирование смешанных и эволюционных стратегий; формирование репутации игроков, в которой фиксируется вся информация о его поведении в прошлом; задание «удовлетворительных» критериев выбора альтернатив;
• выбор единственного равновесия из нескольких равновесных исходов с помощью соглашений и «фокальных точек»; задание критериев выбора альтернатив на основе ценностей; изменение структуры предпочтений индивида.

Олейник А.Н. Институциональная экономика: Учебное пособие. — М.: ИНФРА-М, 2002.